Quantile-Quantile Plots

Quantile-quantile plots are a useful tool for determining whether a measure is normally distributed. From Wikipedia:

Q–Q (quantile-quantile) plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles is chosen. A point (x, y) on the plot corresponds to one of the quantiles of the second distribution (y-coordinate) plotted against the same quantile of the first distribution (x-coordinate). Thus the line is a parametric curve with the parameter which is the number of the interval for the quantile.

Let’s begin with a vector of values, mpg from the mtcars data frame. The plot below is a histogram of values, density of mpg in black, and normal distribution in blue.

data(mtcars)
x <- mtcars$mpg
x <- x[order(x)] # Order the vector
ggplot(mtcars, aes(x = mpg)) + 
    geom_histogram(aes(y = ..density..), bins = 10, fill = 'grey50') +
    geom_density() +
    geom_function(fun = dnorm, 
                  args = list(mean = mean(x), sd = sd(x)),
                  color = 'blue') +
    xlim(mean(x) - 3 * sd(x), mean(x) + 3 * sd(x))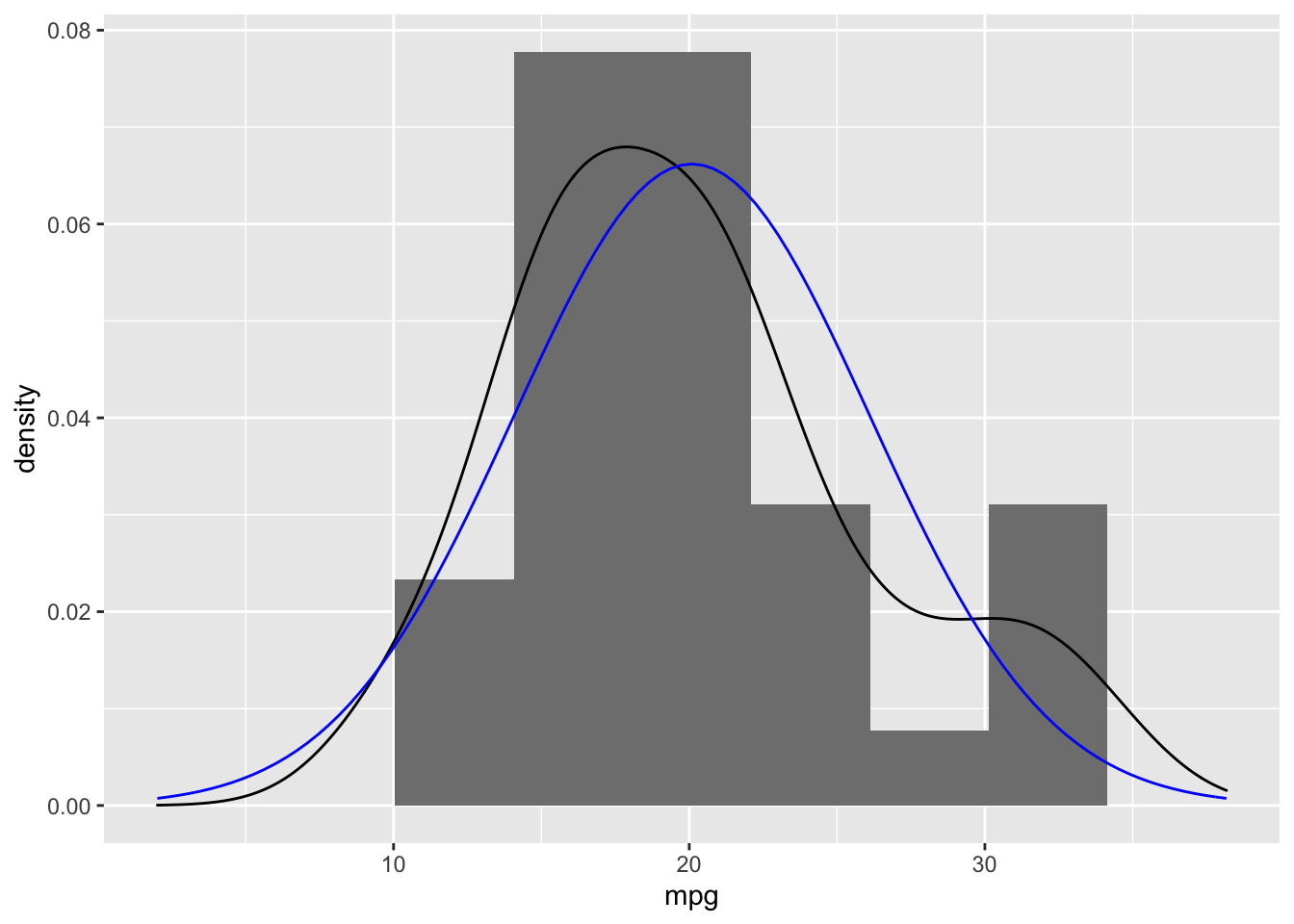

To calculate the theoretical quantiles, we start with a vector of length equal to the original data (i.e. n = 32 in this example). The ppoints generates a sequence of probability points that are equally distributed between 0 and 1.

( points <- ppoints(length(x)) )

##  [1] 0.015625 0.046875 0.078125 0.109375 0.140625 0.171875 0.203125 0.234375
##  [9] 0.265625 0.296875 0.328125 0.359375 0.390625 0.421875 0.453125 0.484375
## [17] 0.515625 0.546875 0.578125 0.609375 0.640625 0.671875 0.703125 0.734375
## [25] 0.765625 0.796875 0.828125 0.859375 0.890625 0.921875 0.953125 0.984375

Using the qnorm function we can calucate the quantile for each of these values.

( y <- qnorm(points) )

##  [1] -2.15387469 -1.67593972 -1.41779714 -1.22985876 -1.07751557 -0.94678176
##  [7] -0.83051088 -0.72451438 -0.62609901 -0.53340971 -0.44509652 -0.36012989
## [13] -0.27769044 -0.19709908 -0.11776987 -0.03917609  0.03917609  0.11776987
## [19]  0.19709908  0.27769044  0.36012989  0.44509652  0.53340971  0.62609901
## [25]  0.72451438  0.83051088  0.94678176  1.07751557  1.22985876  1.41779714
## [31]  1.67593972  2.15387469

mean(y)

## [1] 0

sd(y)

## [1] 0.9960714

Note that the mean and standard deviation are 0 and 1 (within rounding error), respectively, as would be expected from a standard normal distribution. We will no convert our observed values to z-scores and see how they pair up with the theoretical quantiles.

z <- (x - mean(x)) / sd(x)
df <- data.frame(ID = 1:length(x), Observed = x, Observed_z = z, Theoretical = y)
head(df)

##   ID Observed Observed_z Theoretical
## 1  1     10.4 -1.6078826  -2.1538747
## 2  2     10.4 -1.6078826  -1.6759397
## 3  3     13.3 -1.1267104  -1.4177971
## 4  4     14.3 -0.9607889  -1.2298588
## 5  5     14.7 -0.8944204  -1.0775156
## 6  6     15.0 -0.8446439  -0.9467818

ggplot(df, aes(x = Observed_z, y = 'Observed', xend = Theoretical, yend = 'Theoretical')) +
    geom_point(aes(x = Observed_z, y = 'Observed'), color = 'red') +
    geom_point(aes(x = Theoretical, y = 'Theoretical'), color = 'blue') +
    geom_segment() + ylab('') + xlab('')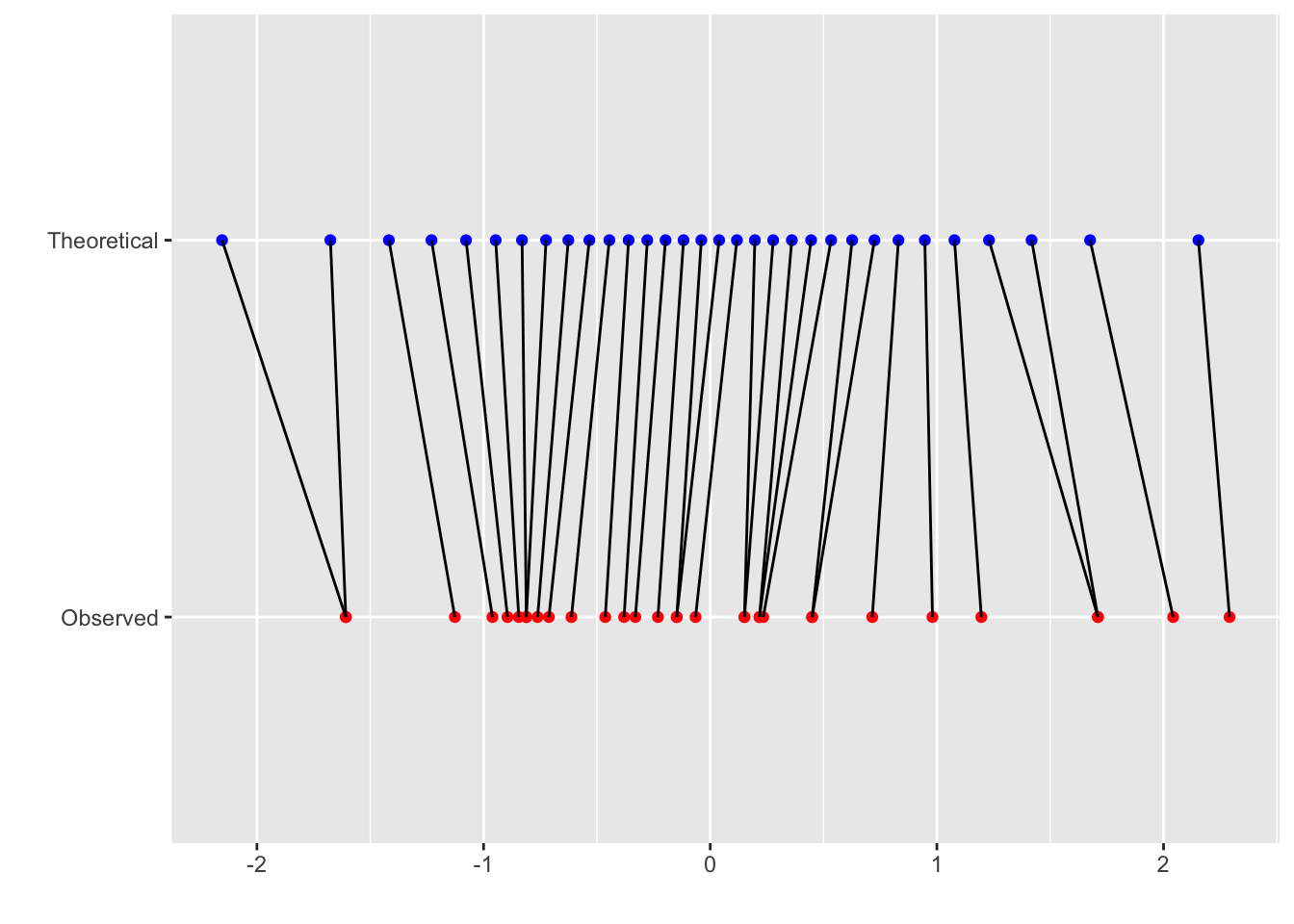

The points in blue are the theoretical quantiles and each is matched to a point in red which is the observed z-score. If the data points were perfectly normal, then all the lines would be vertical. The following plot shows the distributions of these to vectors.

ggplot(data.frame(Observation = c(rep('Observed', length(z)),
                                  rep('Theoretical', length(y))),
                  Value = c(z, y)), aes(x = Value, color = Observation)) +
    geom_density() +
    geom_rug() +
    scale_color_manual(values = c('Observed' = 'red', 'Theoretical' = 'blue')) +
    ylab('') + xlab('z-score')

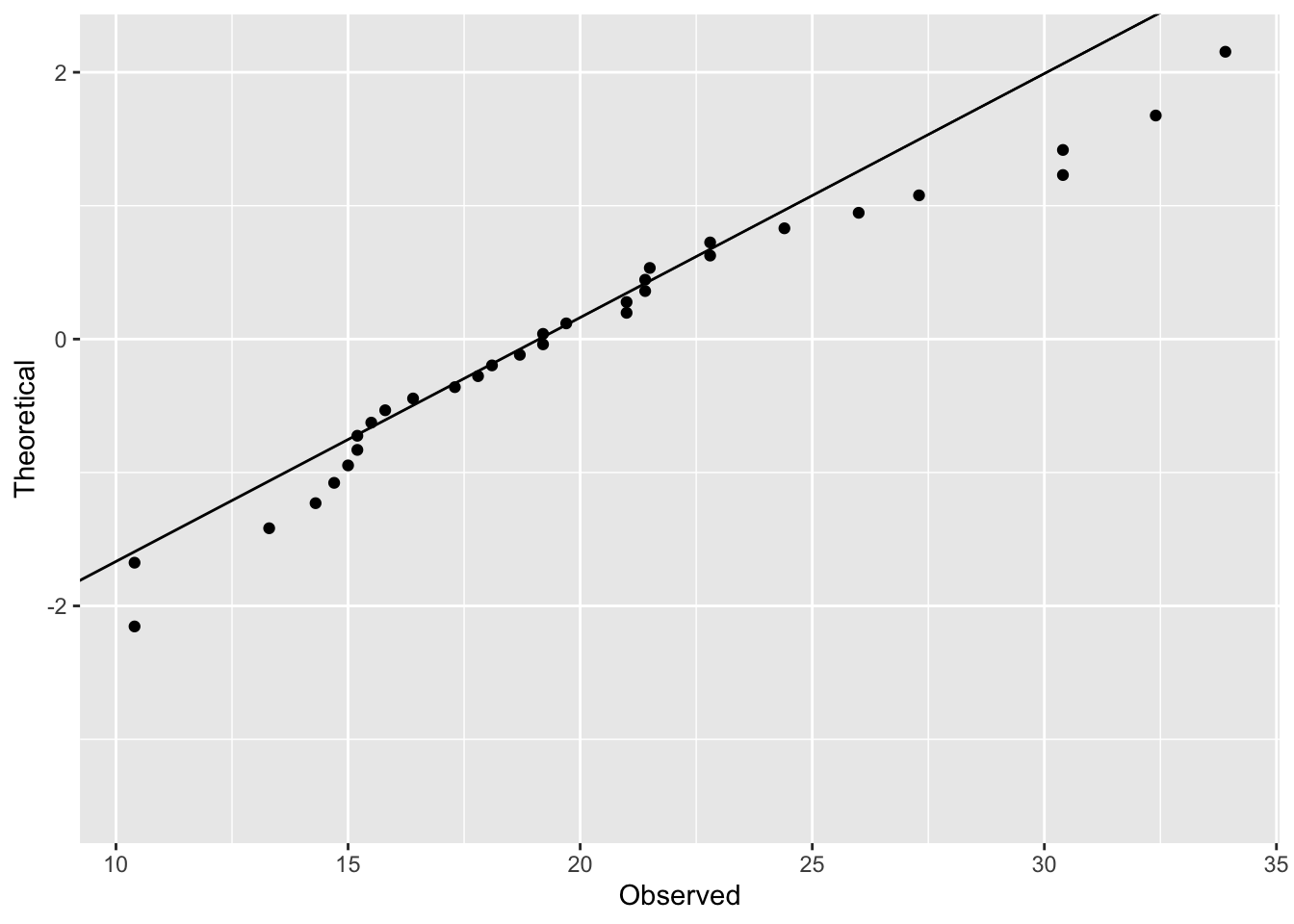
We can see that the distribution does vary from the normal. The q-q plot provides another way of visualizing the departure from the normal distribution.

ggplot(df, aes(x = Observed, y = Theoretical)) + 
    geom_point()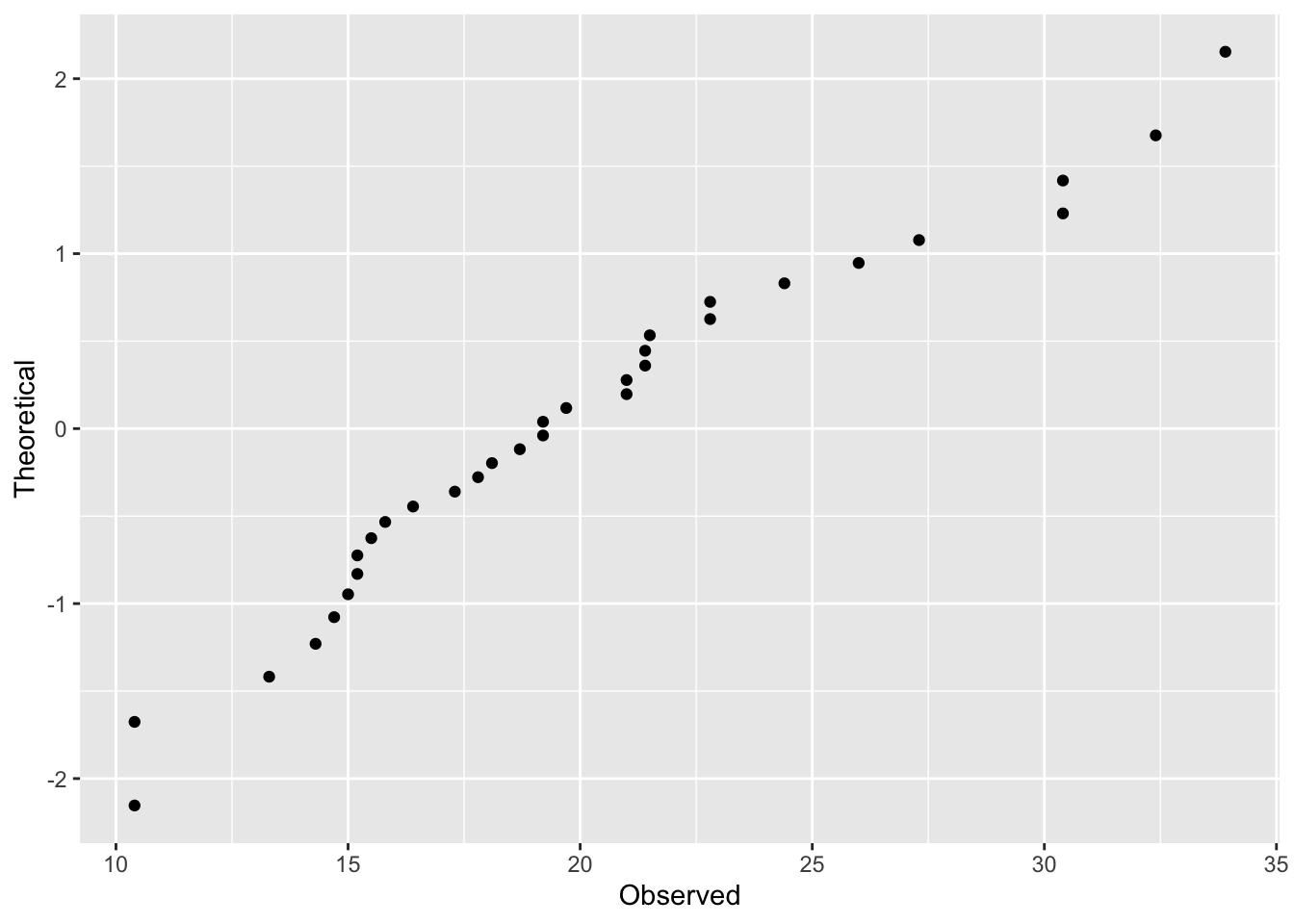

To add the line, we need to calculate the slope and intercept from two points that would fall exactly on the line if the distribution was perfectly normal.

( x2 <- quantile(x, probs = c(0.25, 0.75)) ) # Using 25th and 75th percetile, but any two would work.

##    25%    75% 
## 15.425 22.800

( y2 <- qnorm(c(0.25, 0.75)) )

## [1] -0.6744898  0.6744898

slope <- diff(y2) / diff(x2)
int <- y2[1L] - slope * x2[1L]

ggplot(df, aes(x = Observed, y = Theoretical)) + 
    geom_point() +
    geom_abline(slope = slope, intercept = int)